Results
Contraction
The first experiment was a verification of the contraction dependence on silicone oil concentration. Unilayer films were created with PDMS and silicone oil with dimensions: 1 cm x 2.50 cm x 200 um. The length and width were measured with a ruler before and after contraction. The results were plotted (Figure 1) against the theoretical contraction curves, modeled by the equation: d = 1 - (1- x)⅓, where d is the contraction fraction, and x is the silicone oil concentration (v/v) (Egunov AI et al, 2015).
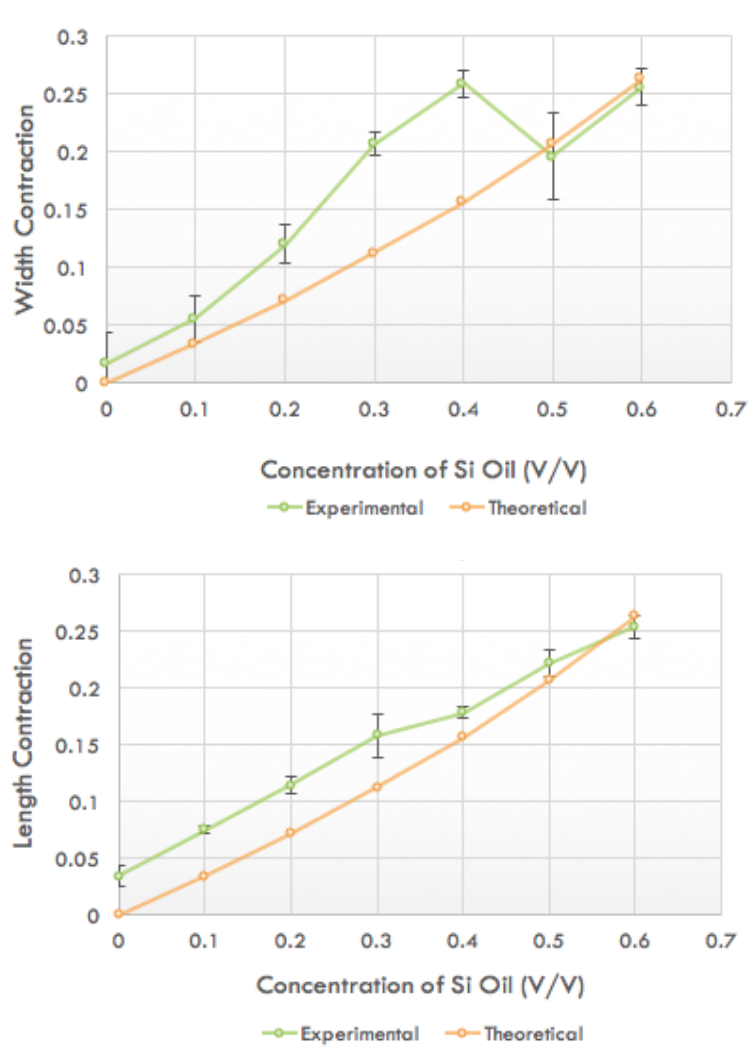
Figure 1. Contraction vs silicone oil concentration in rectangular PDMS, silicone oil films.
Curvature vs Oil Concentration
The curvature against silicone oil concentration was observed in magnetic films. The thickness was kept constant at H = 400um. This was done to be able to compare results to literature results on non-magnetic films (Egunov AI et al, 2015). The silicone oil concentration range used was from 0 to 0.5 (v/v) (Figure 2). A higher concentration than 0.5 made the mixture not viscous enough to be spread on the glass surface. Therefore, the highest concentration tested was 0.5. The measurements were recorded electronically and the plot was created in Excel. The results closely followed the theoretical equation:
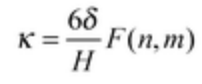
where k is the curvature, 𝛿 is the contraction fraction, H is the total thickness, and F(n,m) is a dimensionless function:
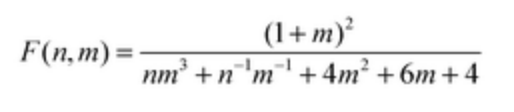
where n = Y1/Y2 (here Yi = Ei/[1 − νi], Ei and νi are the Young modulus and the Poisson ratio of the ith layer), and m = h1/h2 (Egunov AI et al, 2015).
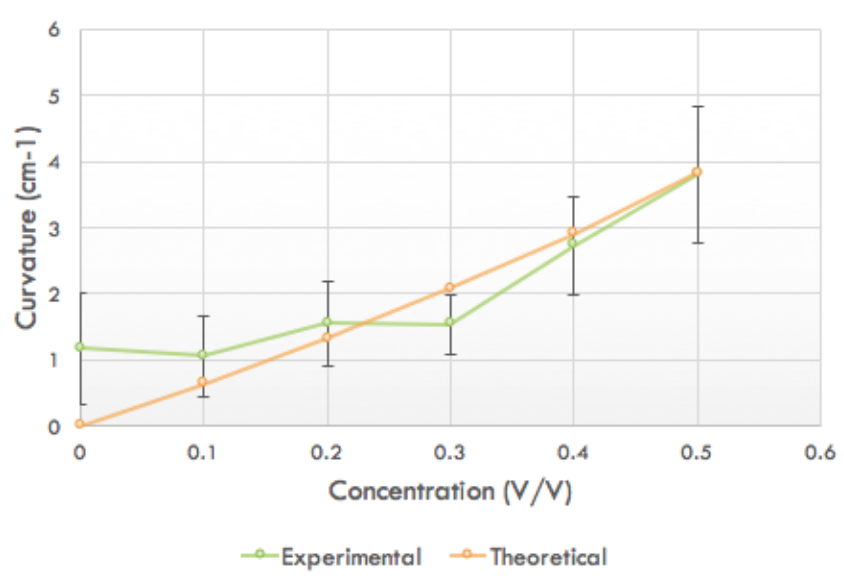
Figure 2. Curvature vs silicone oil concentration in magnetic films. The magnetic films in this experiment had a thickness, H, of 400 um.
Curvature vs Thickness
The curvature against the thickness, H, of the film was investigated. The total thickness range tested was from 200 to 600 um. Three sets of thickness experiments were performed simultaneously with different silicone oil concentrations of 0, 0.2, and 0.4 (Figure 3). The measurements were recorded electronically and the plots were created in Excel. The theoretical curvatures were also plotted using the equation mentioned previously. Some correlation and differentiation is observed in these results.
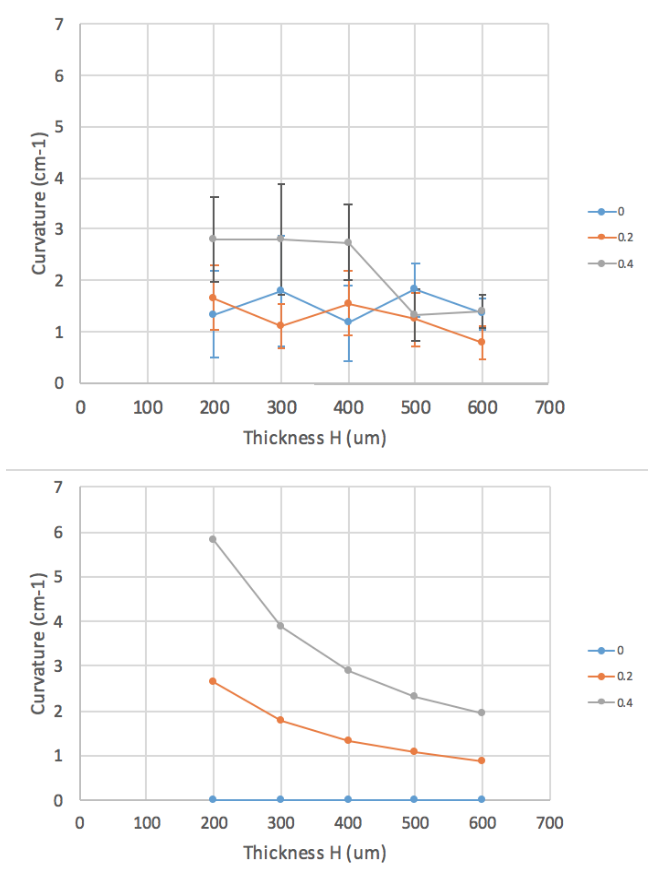
Figure 3. Curvature vs thickness of magnetic films with varying silicone oil concentrations. (Top) Experimental results and (bottom) theoretical values are plotted.
3D Models
After the curvature and contraction of the bilayer magnetic films were characterized, models were created to simulate 3D geometry. The two modes of geometry represent two modes of actuation: crawling and enclosing (Figure 4). An asymmetrical rectangular film, with different curvatures at either ends, k2 > k1, is designed for the crawling mechanism. The different curvatures of the two ends are simulated to produce different push forces at each end after photothermal actuation. On the other hand, the star shape of the second mechanism allows the entrapment of small objects. In both instances, the force of the magnet initially forces the magnetic films to lie flat on the surface. After photothermal actuation using a laser, the magnetic films return to their spontaneous curvature states.
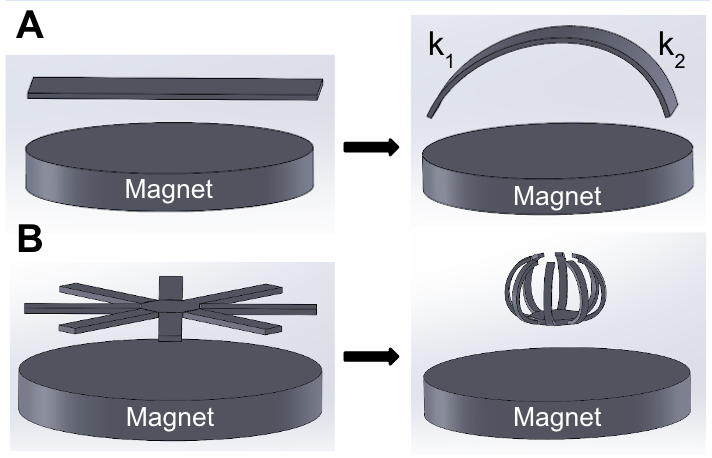
Figure 4. 3D models of the actuating geometry. (A) A crawling and (B) an enclosing mechanisms of actuation were modeled using Solidworks.